План- конспект урока
Решение уравнений (Тема урока)
ФИО (полностью): Ковлагина Марина Игоревна
Место работы:
МБОУ СОШ № 2 г. Лакинска Собинского района Владимирской области
Должность: учитель математики
Предмет: математика
Класс: 9 класс
Тема и номер урока в теме Решений уравнений
Базовый учебник А.Г. Мордкович,. Алгебра, 9 класс
Цель урока: обобщить и привести в систему имеющиеся знания по теме “Решение уравнений,; помочь учащимся выявить и устранить пробелы в знаниях по теме;
Задачи:
- обучающие:
- Систематизировать, расширить и углубить знании и умения учащихся в применении алгоритмов решения уравнений.
- Способствовать развитию наблюдательности, умению анализировать, сравнивать, делать выводы.
- Побуждать учеников к само- и взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
- Закрепить правила нахождения и вычисления корней уравнений;
- Сформировать навыки вычислительных задач с корнями уравнений;
-развивающие:
- Развитие логического мышления;
- Развитие интеллекта через заучивание математических терминов;
- Развитие навыков самоорганизации;
- Развитие воли через задание посильной сложности;
-воспитательные :
- Воспитывать аккуратность записей;
- Воспитывать уважительное отношение друг к другу.
- Тип урока: урок - тренинг
- Формы работы учащихся :индивидуальная, групповая
- Необходимое техническое оборудование: компьютер, экран, мультимедийный проектор
Просмотр содержимого документа
«Ковлагина М.И.- План конспект урока»
Просмотр содержимого документа
«задания для урока»
Просмотр содержимого презентации
«ГИА 2013. Модуль АЛГЕБРА (№4)»
Решение уравнений
Решите уравнение:
2 – 3*(2х + 2) = 5 – 4х
2 – 6х – 6 = 5 – 4х
-6х + 4х =5 – 6 + 2
х = 1 : (-2)
х= - 0,5
Ответ:
5
,
0
-
0, 2 корня х 1 = = - 3 х 2 = = 5 Ответ: 3 ; 5 -" width="640"
Х 2 + 2х – 15 = 0
а = 1; b = 2; с = - 15
D = 2 2 – 4*1*(-15) = 64, D 0, 2 корня
х 1 = = - 3
х 2 = = 5
Ответ:
3
;
5
-
= * (х – 3), где х ≠ 3
х 2 – 6 = х
х 2 – х – 6 = 0
по теореме, обратной теореме Виета
х 1 + х 2 = 1;
х 1 * х 2 = - 6;
значит х 1 = - 2 и х 2 = 3.
Ответ:
2
-
;
3
- Линейное уравнение: ах + b = 0;
- Квадратное уравнение: ах 2 + b х + с = 0;
- Рациональное уравнение: р(х) = 0, где р(х) – рациональное выражение;
- Иррациональное уравнение: =0.
Решите уравнение
7
Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена.
Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить (вычесть) числители.
Чтобы умножить обыкновенные дроби, надо перемножить отдельно числители и знаменатели.
Чтобы выделить целую часть из неправильной дроби, надо числитель разделить на знаменатель, неполное частное – целая часть, остаток – числитель, знаменатель без изменения
7
Решите уравнение
▪ (2-х), где 2-х≠0; х≠2
9
Дробно-рациональное уравнение имеет смысл тогда, когда знаменатель дробей, входящих в уравнение, не равен нулю.
Дробно-рациональное уравнение можно свести к целому, если обе его части умножить на общий знаменатель.
9
0, ⇒ 2 корня 11" width="640"
Решите уравнение
D 0, ⇒ 2 корня
11
0, то уравнение имеет два корня. Корни квадратного уравнения можно вычислить по формулам: 11" width="640"
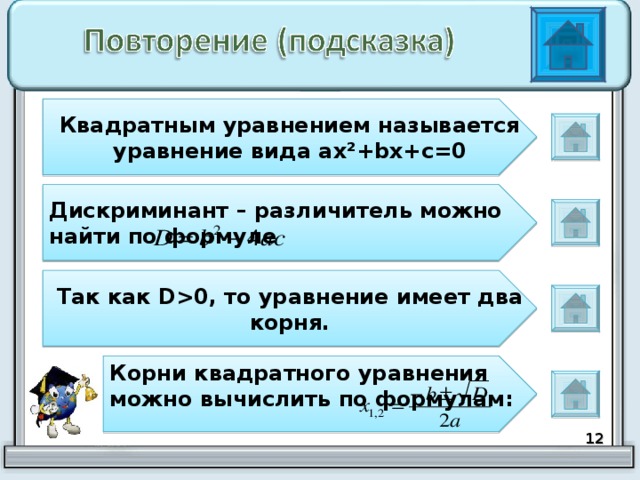
Квадратным уравнением называется уравнение вида ax ²+bx+c=0
Дискриминант – различитель можно найти по формуле
Так как D 0, то уравнение имеет два корня.
Корни квадратного уравнения можно вычислить по формулам:
11
Молодцы!
Спасибо за работу!
= 
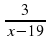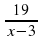
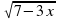= х + 7
= 
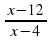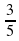
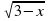= 3х + 5
= 
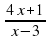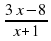
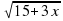= 1 - х 
= 
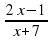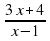
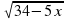= 7 - 2х 
