Геометрические задачи на вычисление

Материал для учащихся девятых классов. Представлены задачи по геометрии на вычисление. Задания помогут учащимся при подготовке к ОГЭ. Примеры задач на нахождение медианы прямоугольного теругольника, вычисления радиуса окружности, задачи на вычисление отрезков в трапеции, вычисление угла между высотой и биссектрисой в прямоугольном треугольнике, вычисление площадей прямоугольника, трапеции.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Геометрические задачи на вычисление »

Геометрические задачи на вычисление.

1. В прямоугольном треугольнике с прямым углом известны катеты:

, . Найдите медиану этого треугольника.

Решение.

Медиана, проведенная к гипотенузе, равна её половние:

Ответ: 5.

2. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 100°.

Решение.

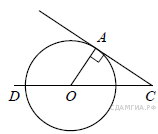Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 100° = 80°; ∠ACO = 90° − 80° = 10°.

Ответ: 10.

3. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.

Решение.

Опустим радиусы на каждую касательную. Соединим точки A и O. Получившиеся треугольники - прямоугольные, так как радиус, проведенный в точку касания, перпендикулярен касательной. По гипотенузе и катету эти треугольники равны, таким образом, мы получили, что угол, лежащий напротив катета равен Катет, лежащий напротив угла в равен половине гипотенузы, тогда радиус равен 4.

Ответ: 4.

4. В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

Решение.

Так как AB = CD, то трапеция является равнобедренной. Опустим перпендикуляр BL из точки B на большее основание AD. Прямоугольные треугольники ABL и CHD равны по гипотенузе и прилежащему острому углу, поэтомуAL = HD. Средняя линия равна полусумме оснований:

Так как отрезки AL=HD, то , значит,

Ответ: HD = 12.

5. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.

Решение.

Найдем

Так как BD - биссектриса, то

Треугольник HBC- прямоугольный. Так как то

Таким образом, искомый угол DBH равен

Ответ:

6. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.

Решение.

Так как высота AD, проведенная к медиане BM делит ее пополам, то треугольник ABM является равнобедренным, поэтому AB=AM=4. Так как BM- медиана, то AM=MC, таким образом, AC=2AM=8.

Ответ: AC=8.

7. На сторонах угла , равного 20°, и на его биссектрисе отложены равные отрезки , и . Определите величину угла .

Решение.

Так как отрезки равны, то треугольники ACD и ABD - равнобедренные. Углы при основании этих треугольников равны:

Найдем искомый угол:

Ответ:

8. Найдите величину угла , если — биссектриса угла , — биссектриса угла .

Решение.

Имеем: = 2 · 25° = 50°; = 180° − 50° = 130°; = 130° : 2 = 65°.

Ответ: 65°.

9. Основание равнобедренной трапеции равны 8 и 18, а её периметр равен 52. Найдите площадь трапеции.

Решение.

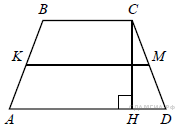
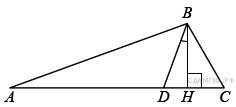
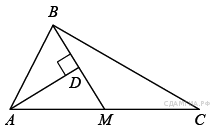
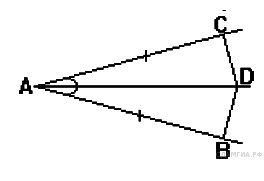
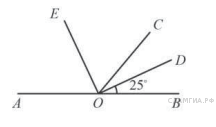
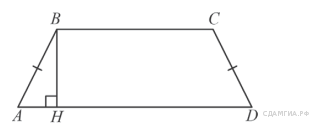Рассмотрим равнобедренную трапецию с основаниями и , периметр которой равен 52. Имеем

Пусть — высота трапеции. Тогда . Из прямоугольного треугольника находим . Значит, площадь трапеции равна .

Ответ: 156.

10. Периметр прямоугольника равен 56, а диагональ равна 27. Найдите площадь это прямоугольника.

Решение.

Пусть одна из сторон прямоугольника равна . Тогда другая сторона равна , а площадь . По теореме Пифагора:

Значит, искомая площадь равна 27,5.

Ответ: 27,5.

Предмет: Математика

Категория: Уроки

Целевая аудитория: 9 класс

Скачать
Геометрические задачи на вычисление

Автор: Хакимзянова Нурания Идерисовна

Дата: 06.11.2014

Номер свидетельства: 127420

Похожие файлы

Пути и способы осуществления дифференциации обучения при формировании обобщенного приема решения задач

object(ArrayObject)#854 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(193) "Пути и способы осуществления дифференциации обучения при формировании обобщенного приема решения задач"
    ["seo_title"] => string(126) "puti-i-sposoby-osushchiestvlieniia-diffierientsiatsii-obuchieniia-pri-formirovanii-obobshchiennogho-priiema-rieshieniia-zadach"
    ["file_id"] => string(6) "314650"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1459751208"
  }
}

конспект урока на тему "Решение задач на применение признаков равенства треугольников"

object(ArrayObject)#876 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(161) "конспект урока на тему "Решение задач на применение признаков равенства треугольников" "
    ["seo_title"] => string(97) "konspiekt-uroka-na-tiemu-rieshieniie-zadach-na-primienieniie-priznakov-ravienstva-trieughol-nikov"
    ["file_id"] => string(6) "167717"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1423132835"
  }
}

Роль компетентностно-ориентированных задач в формировании математической грамотности учащихся

object(ArrayObject)#854 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(178) "Роль компетентностно-ориентированных задач в формировании математической грамотности учащихся"
    ["seo_title"] => string(80) "rol_kompietientnostno_oriientirovannykh_zadach_v_formirovanii_matiematichieskoi_"
    ["file_id"] => string(6) "420280"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1496495945"
  }
}

Применение задач с профессиональной направленностью на уроках математики

object(ArrayObject)#876 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(137) "Применение задач с профессиональной направленностью на уроках математики"
    ["seo_title"] => string(81) "primienieniie-zadach-s-profiessional-noi-napravliennost-iu-na-urokakh-matiematiki"
    ["file_id"] => string(6) "283997"
    ["category_seo"] => string(10) "matematika"
    ["subcategory_seo"] => string(7) "prochee"
    ["date"] => string(10) "1453909123"
  }
}

Урок математики на тему "Решение задач", 2 класс

object(ArrayObject)#854 (1) {
  ["storage":"ArrayObject":private] => array(6) {
    ["title"] => string(86) "Урок математики на тему "Решение задач", 2 класс "
    ["seo_title"] => string(52) "urok-matiematiki-na-tiemu-rieshieniie-zadach-2-klass"
    ["file_id"] => string(6) "233829"
    ["category_seo"] => string(16) "nachalniyeKlassi"
    ["subcategory_seo"] => string(5) "uroki"
    ["date"] => string(10) "1443243808"
  }
}

Геометрические задачи на вычисление

Просмотр содержимого документа «Геометрические задачи на вычисление »

Похожие файлы

Полезное для учителя

Просмотр содержимого документа
«Геометрические задачи на вычисление »