Математика, 9 класс. Подготовка к ОГЭ, задания 5 и 23.
ОГЭ
Задание 5
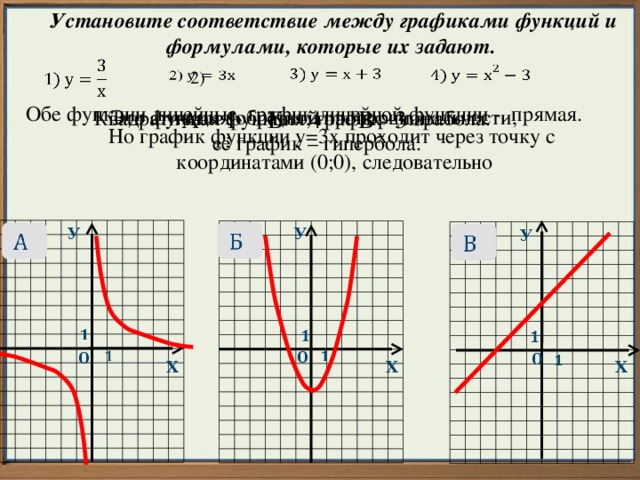
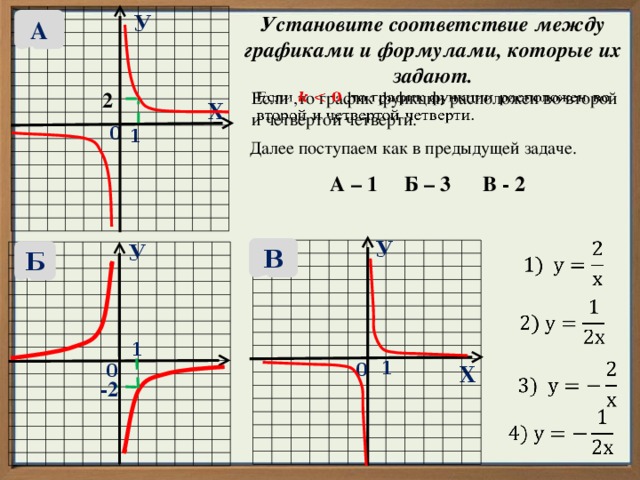
Установите соответствие между графиками функций и формулами, которые их задают.
2)
Обе функции линейные, график линейной функции - прямая.
Это функция обратной пропорциональности,
её график – гипербола.
А – 1 Б – 4 В - 3
Квадратичная функция, график – парабола.
Но график функции у=3х проходит через точку с
координатами (0;0), следовательно
У
У
У
0
0
0
Х
Х
Х
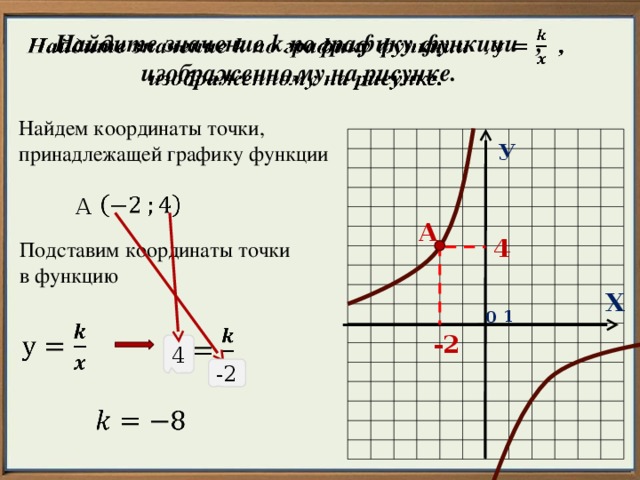
Найдите значение k по графику функции , изображенному на рисунке.
Найдем координаты точки, принадлежащей графику функции
У
А
А
4
Подставим координаты точки
в функцию
Х
1
0
-2
4
-2
У
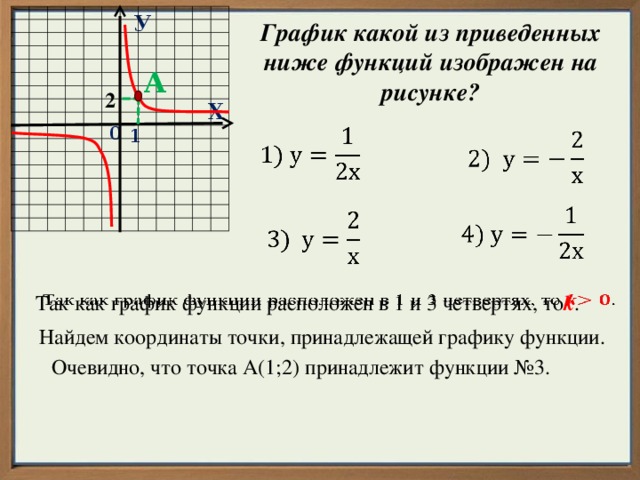
График какой из приведенных ниже функций изображен на рисунке?
А
2
Х
0
1
Так как график функции расположен в 1 и 3 четвертях, то k
Найдем координаты точки, принадлежащей графику функции.
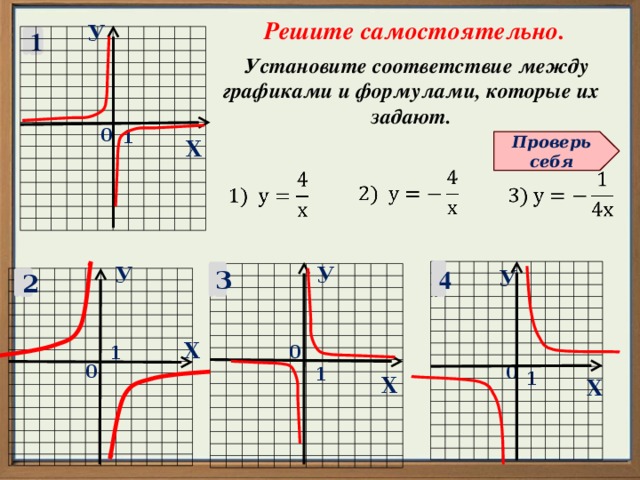
Очевидно, что точка А(1;2) принадлежит функции №3.
Установите соответствие между графиками и формулами, которые их задают.
У
А
Если ,то график функции расположен во второй и четвертой четверти.
2
Х
0
1
Далее поступаем как в предыдущей задаче.
А – 1 Б – 3 В - 2
У
У
В
Б
1
1
0
0
Х
-2
Решите самостоятельно.
У
1
Установите соответствие между графиками и формулами, которые их задают.
0
1
Х
Проверь себя
У
У
4
У
3
2
Х
0
1
0
0
1
1
Х
Х
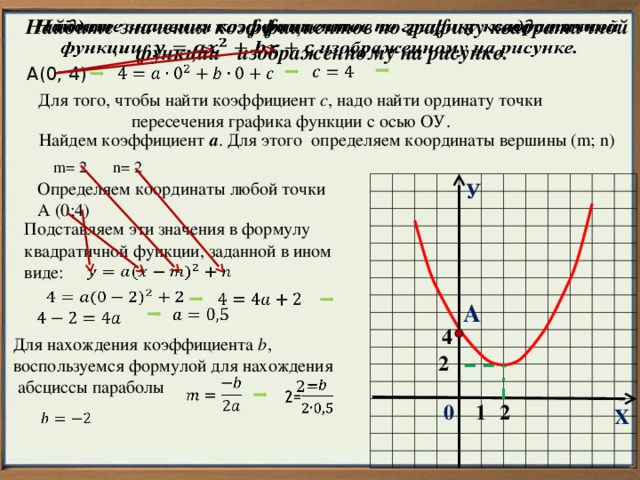
Найдите значения коэффициентов по графику квадратичной функции изображенному на рисунке.
А(0; 4)
Для того, чтобы найти коэффициент c , надо найти ординату точки пересечения графика функции с осью ОУ.
Найдем коэффициент а
n= 2
m= 2
У
Определяем координаты любой точки
А (0;4)
Подставляем эти значения в формулу квадратичной функции, заданной в ином виде:
А
4
Для нахождения коэффициента b ,
воспользуемся формулой для нахождения
абсциссы параболы
2
2=
2
1
0
Х
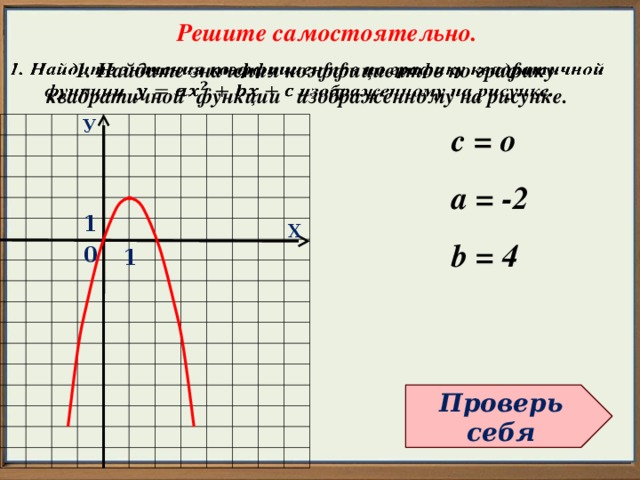
Решите самостоятельно.
1. Найдите значения коэффициентов по графику квадратичной функции изображенному на рисунке.
У
с = о
а = -2
b = 4
1
Х
0
1
Проверь себя
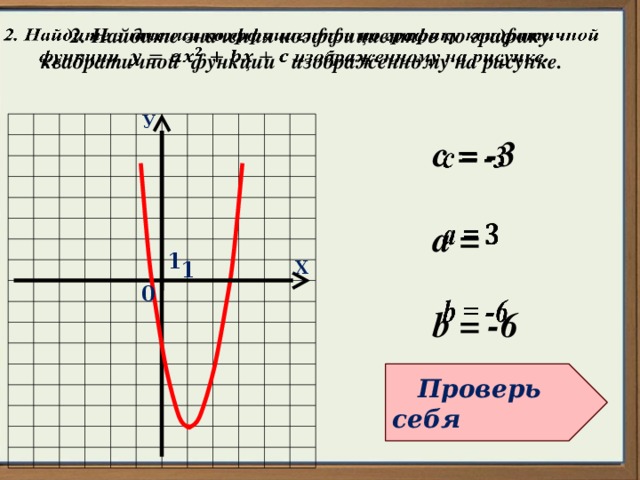
2. Найдите значения коэффициентов по графику квадратичной функции изображенному на рисунке.
У
с = -3
а =
b = -6
1
Х
1
0
Проверь себя
ОГЭ
Задание 23
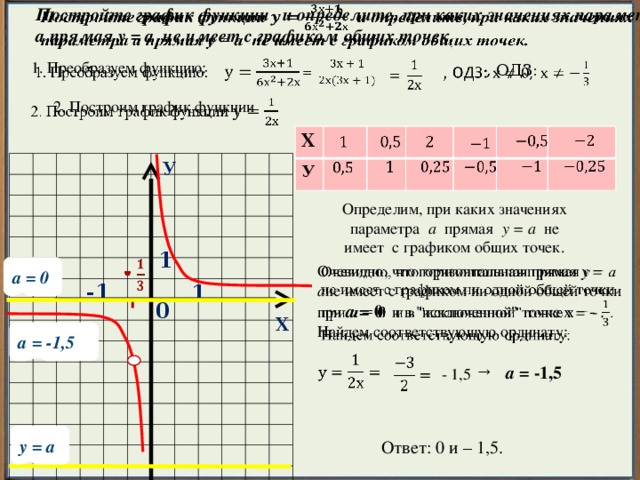
Постройте график функции и определите, при каких значениях параметра а прямая у = а не имеет с графиком общих точек.
1. Преобразуем функцию:
, ОДЗ:
2. Построим график функции
Х
У
1
У
Определим, при каких значениях параметра а прямая у = а не имеет с графиком общих точек.
1
-
а = 0
Очевидно, что горизонтальная прямая y = а не имеет с графиком ни одной общей точки при а = 0 и в "исключенной" точке x = - .
Найдем соответствующую ординату:
-1
1
0
Х
а = -1,5
а = -1,5
- 1,5
у = а
Ответ: 0 и – 1,5.
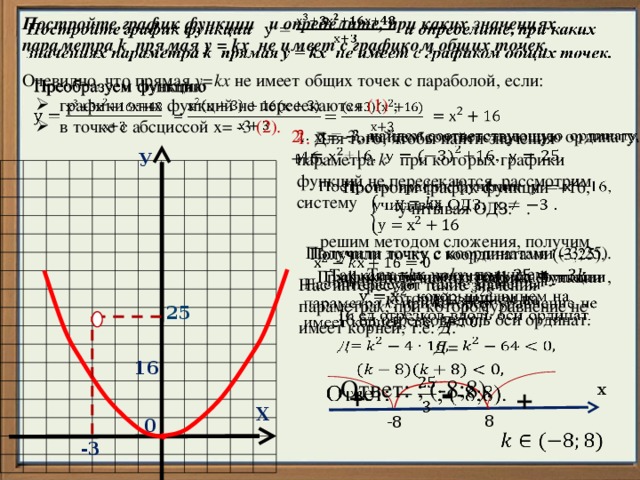
Постройте график функции и определите, при каких значениях параметра k прямая у = kх не имеет с графиком общих точек.
Очевидно, что прямая у=kх не имеет общих точек с параболой, если:
Преобразуем функцию
графики этих функций не пересекаются (1) ; в точке с абсциссой х= -3 (2).
2 . х = -3, найдем соответствующую ординату.
+16, , .
1. Для того, чтобы найти значения параметра k при которых графики функций не пересекаются, рассмотрим систему
У
Построим график функции +16, учитывая ОДЗ: .
решим методом сложения, получим
Получили точку с координатами (-3;25).
Так как у=kх, получаем
График получим из графика функции , который сдвинем на
16 ед.отрезковвдоль оси ординат.
Нас интересуют такие значения параметра k , при которомуравнение не имеет корней, т.е. Д.
25
Д=
16
-
Ответ: ; (-8;8).
+
х
+
Х
8
-8
0
-3
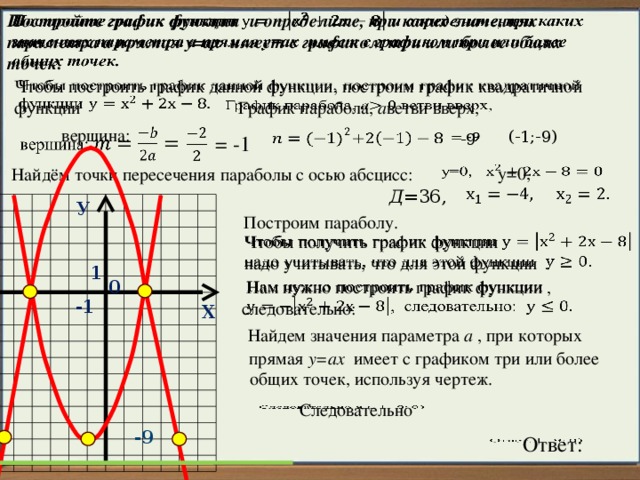
Постройте график функции и определите, при каких значениях параметра а прямая у=ах имеет с графиком три или более общих точек.
Чтобы построить график данной функции, построим график квадратичной функции
График парабола, а ветви вверх,
вершина:
(-1;-9)
-9
= -1
у=0,
Найдём точки пересечения параболы с осью абсцисс:
Д =36,
У
Построим параболу.
Чтобы получить график функции
надо учитывать, что для этой функции .
1
Нам нужно построить график функции , следовательно:
0
-1
Х
Найдем значения параметра а , при которых
прямая у=ах имеет с графиком три или более
общих точек, используя чертеж.
Следовательно
-9
Ответ:
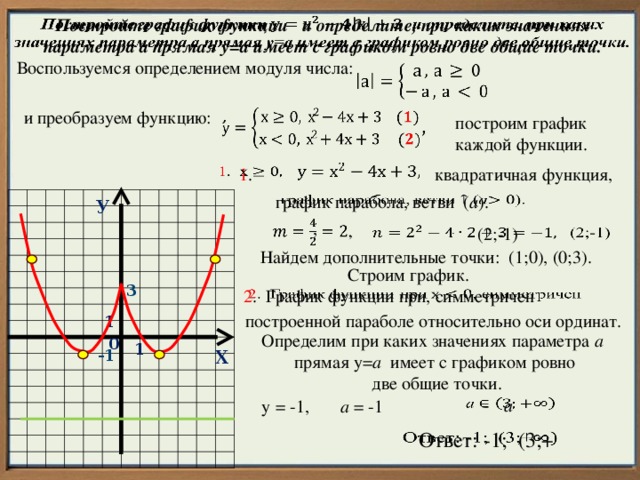
Постройте график функции и определите, при каких значениях параметра а прямая у=а имеет с графиком ровно две общие точки.
Воспользуемся определением модуля числа:
,
и преобразуем функцию:
построим график
каждой функции.
1 .
квадратичная функция,
график парабола, ветви ( а ).
У
,
(2;-1)
Найдем дополнительные точки: (1;0), (0;3).
Строим график.
3
2 . График функции при, симметричен
построенной параболе относительно оси ординат.
1
Определим при каких значениях параметра а
прямая у= а имеет с графиком ровно
две общие точки.
0
1
-1
Х
а
у = -1, а = -1
Ответ: -1; (3;+
Самостоятельная работа.
1. Постойте график функции у= и определите , при каких значениях параметра а прямая у=а не имеет с графиком общих точек.
Проверь решение
2. Постройте график функции и определите, при каких
значениях параметра а прямая а имеет с графиком ровно две
общие точки.
Проверь решение
3. Постройте график функции и определите , при каких значениях параметра а прямая у=а имеет с графиком три или более общих точек.
Проверь решение
4. Постройте график функции у= и определите, при каких значениях параметра k прямая у=kх не имеет с графиком общих точек.
Проверь решение
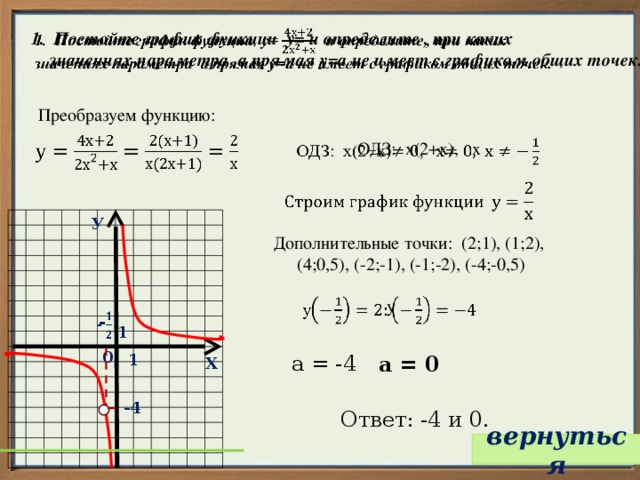
1. Постойте график функции у= и определите , при каких значениях параметра а прямая у=а не имеет с графиком общих точек.
Преобразуем функцию:
ОДЗ: х(2+х), х
У
Дополнительные точки: (2;1), (1;2),
(4;0,5), (-2;-1), (-1;-2), (-4;-0,5)
у
-
1
0
1
а = -4
а = 0
Х
-4
Ответ: -4 и 0.
вернуться
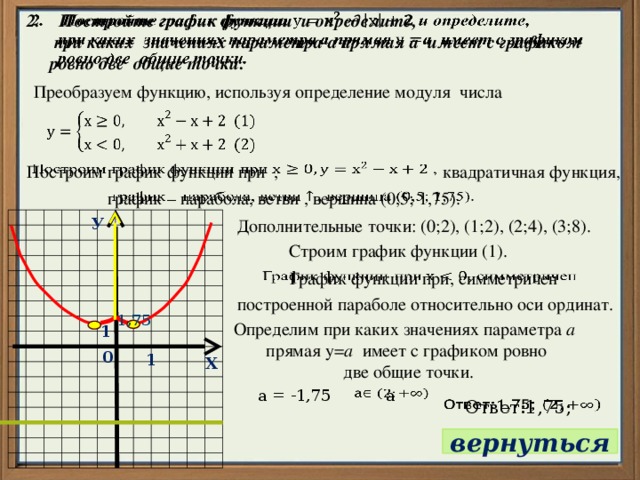
Постройте график функции и определите,
при каких значениях параметра а прямая а имеет с графиком
ровно две общие точки.
Преобразуем функцию, используя определение модуля числа
Построим график функции при ,
квадратичная функция,
график – парабола, ветви , вершина (0,5; 1,75).
У
Дополнительные точки: (0;2), (1;2), (2;4), (3;8).
Строим график функции (1).
График функции при, симметричен
построенной параболе относительно оси ординат.
1,75
Определим при каких значениях параметра а
прямая у= а имеет с графиком ровно
две общие точки.
1
0
1
Х
а = -1,75
а
Ответ:1,75;
вернуться
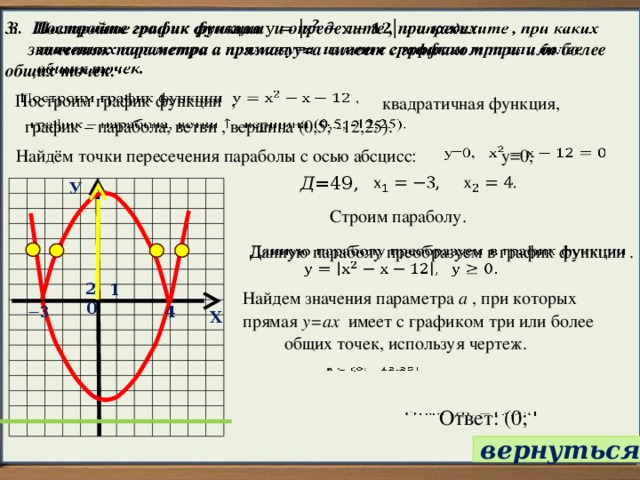
3. Постройте график функции и определите , при каких
значениях параметра а прямая у=а имеет с графиком три или более
общих точек.
Построим график функции ,
квадратичная функция,
график – парабола, ветви , вершина (0,5; -12,25).
Найдём точки пересечения параболы с осью абсцисс:
у=0,
Д =49,
У
Строим параболу.
Данную параболу преобразуем в график функции .
2
1
Найдем значения параметра а , при которых
0
4
Х
прямая у=ах имеет с графиком три или более
общих точек, используя чертеж.
Ответ: (0;
вернуться
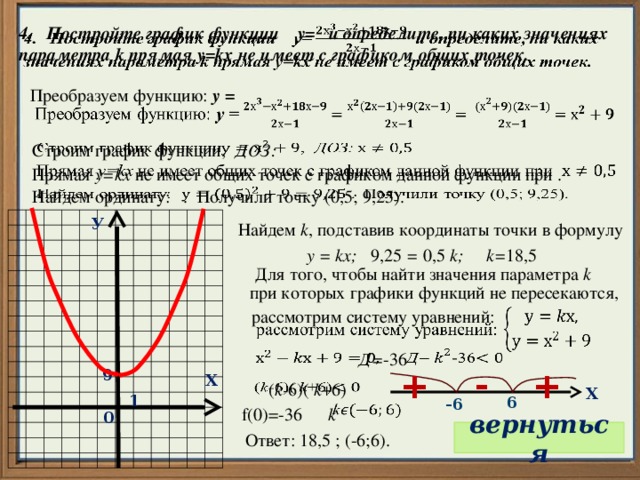
4. Постройте график функции у= и определите, пи каких значениях параметра k прямая у=kх не имеет с графиком общих точек.
Преобразуем функцию: у =
Прямая у=kх не имеет общих точек с графиком данной функции при .
Строим график функции, ДОЗ:
Найдем ординату: . Получили точку (0,5; 9,25).
У
Найдем k , подставив координаты точки в формулу
у = kх; 9,25 = 0,5 k; k= 18,5
Для того, чтобы найти значения параметра k
при которых графики функций не пересекаются,
рассмотрим систему уравнений:
Д= -36
-
+
+
9
Х
( k- 6)( k +6)
Х
k
1
6
-6
f(0)=-36
0
вернуться
Ответ: 18,5 ; (-6;6).
Удачи на экзамене!!!