Формы урока: урок изучения нового материала.
Цель урока: рассмотреть простейшие задачи в координатах и показать, как они применяются при решении задач.
Форма работы: фронтальная.
Оборудование: проектор, компьютер.
Методы: проблемно-поисковый, словесный, индуктивный.
Ход урока
I. Приветствие.
II. Сообщение учителем цели урока.
III. Фронтальная работа с классом.
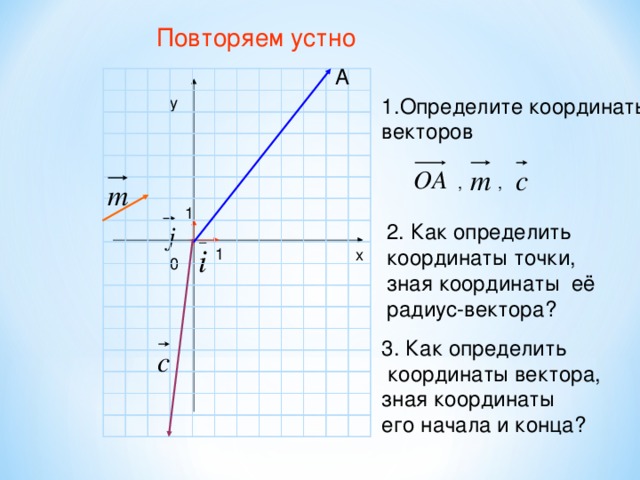
На прошлых уроках мы выяснили, что такое радиус-вектор, и как его координаты связаны с координатами точки, в которую он проведён. Также вы уже знаете, как вычислить координаты вектора, зная координаты его начала и конца. Вспомните соответствующие утверждения и выполните задания – слайды №2 и №3.
Введение системы координат позволяет использовать алгебраические методы при решении геометрических задач. Такой подход к изучению свойств геометрических фигур называется методом координат. Сегодня мы познакомимся с тремя вспомогательными задачами, на которых основывается метод координат.
Далее, разбирая с учащимися возникшую проблему, учитель координирует и направляет их работу, добиваясь от учащихся самостоятельности мышления и осознанного применения соответствующих формул.
1)
А) Учитель формулирует проблему; как, зная координаты концов отрезка, вычислить координаты его середины? В ходе коллективного обсуждения вырабатывается план решения, учащиеся делают записи в тетрадях – слайд №4. Учитель предлагает учащимся самостоятельно сформулировать утверждение. Если они затрудняются – им в помощь слайд №5.
Б) Для закрепления полученной формулы учитель предлагает учащимся устно решить задачи со слайда №6. Если класс слабый, то один из учеников может комментировать решение с места, а остальные делают записи в тетрадях. Если класс сильный, то можно проверить только ответы – слайды №16 и №17.
2)
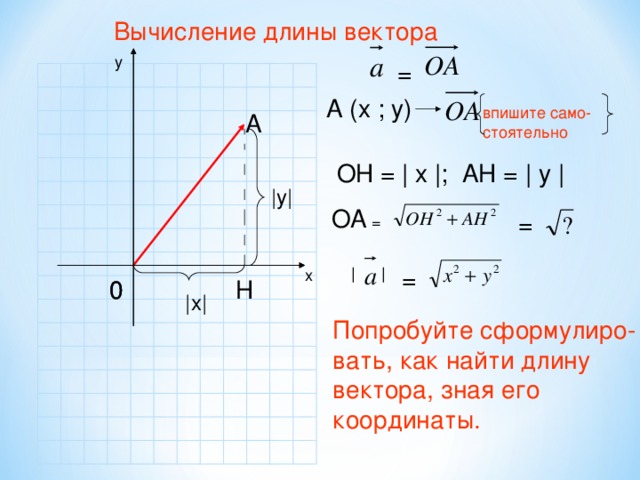
А) Учитель формулирует проблему; как, зная координаты вектора, вычислить его длину? В ходе обмена мнениями и коллективного обсуждения появляется план решения. В помощь учащимся слайд №7. Затем учитель просит учащихся сформулировать полученное утверждение. Для этого в помощь учащимся слайд №8.
Б) Для закрепления полученной формулы учитель предлагает учащимся устно решить задачи со слайда №9. Если класс слабый, то один из учеников может комментировать решение с места, а остальные делают записи в тетрадях. Если класс сильный, то можно проверить только ответы – слайды №10 и №11.
3)
А) Учитель формулирует проблему; как, зная координаты точек, вычислить расстояние между ними? В ходе обсуждения появляются записи в тетрадях. В помощь учащимся слайд №12.
Б) Для первичного закрепления учащимся предлагается устно решить задачи со слайда №13. Если возникнут затруднения, то решения и ответы есть на слайдах №14 и №15.
IV. Запись домашнего задания:
слайд №18.
V. Подведение итогов урока, выставление оценок