ПРЕОБРАЗОВАНИЕ ЛОГАРИФМИЧЕСКИХ ВЫРАЖЕНИЙ
- Логарифмом числа b по основанию a называется такой показатель степени, в которую нужно возвести число a, чтобы получить число b.
- Свойства логарифмов
-
Формулы перехода
-
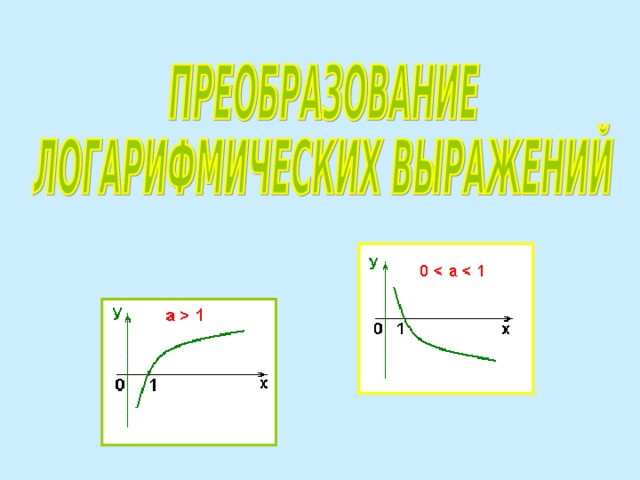
Логарифмическая функция.
-
Логарифмические уравнения
-
Логарифмические неравенства
 0, a≠1, b0" width="640"
0, a≠1, b0" width="640"
 0, a ≠1, b 0, с0, r – любое действительное число) Основное логарифмическое тождество: log a ( bc ) = log a b + log a c log a ( b / c ) = log a b – log a c log a b ⁿ = n*log a b log a ⁿ b = 1/ n*log a b 6) log a ⁿ b ⁿ = log a b" width="640"
0, a ≠1, b 0, с0, r – любое действительное число) Основное логарифмическое тождество: log a ( bc ) = log a b + log a c log a ( b / c ) = log a b – log a c log a b ⁿ = n*log a b log a ⁿ b = 1/ n*log a b 6) log a ⁿ b ⁿ = log a b" width="640"
 0,a≠1, b0, c0, c≠1 Формула перехода к другому основанию log a bⁿ = log n bª log c b log c a a = b" width="640"
0,a≠1, b0, c0, c≠1 Формула перехода к другому основанию log a bⁿ = log n bª log c b log c a a = b" width="640"
 0, a ≠1, x 0, называется логарифмической функцией ; ООФ: x 0; МЗФ : y є R ; Функция общего вида ; 0 a1 ООФ: x0; МЗФ: y є R; Функция убывает на промежутке x 0 ООФ: x0; МЗФ: y є R; Функция возрастает на промежутке x 0 График логарифмической функции всегда проходит через точку (1;0) Логарифмическая функция - обратная для показательной функции" width="640"
0, a ≠1, x 0, называется логарифмической функцией ; ООФ: x 0; МЗФ : y є R ; Функция общего вида ; 0 a1 ООФ: x0; МЗФ: y є R; Функция убывает на промежутке x 0 ООФ: x0; МЗФ: y є R; Функция возрастает на промежутке x 0 График логарифмической функции всегда проходит через точку (1;0) Логарифмическая функция - обратная для показательной функции" width="640"
 0, a ≠1, x 1 0, x 2 0, то X 1 = X 2 . Способы решения:" width="640"
0, a ≠1, x 1 0, x 2 0, то X 1 = X 2 . Способы решения:" width="640"
 log a g(x) 0 a1 f(x) f(x) 0 f(x) g(x) g(x) 0 log a(x) f(x) log a(x) g(x) 0f(x) f(x) 0 a(x) 1, f(x) g(x), g(x) 0" width="640"
log a g(x) 0 a1 f(x) f(x) 0 f(x) g(x) g(x) 0 log a(x) f(x) log a(x) g(x) 0f(x) f(x) 0 a(x) 1, f(x) g(x), g(x) 0" width="640"















