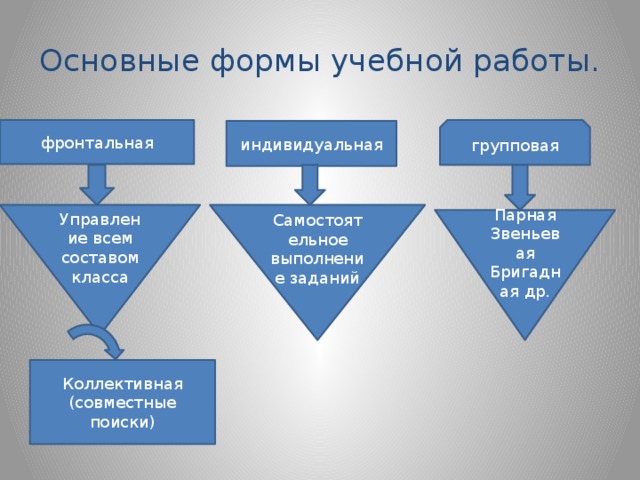
Методика применения элементов парацентрической технологии на уроках математики

Методика применения элементов парацентрической технологии на уроках по математике.

Тезис принять за аксиому:

Человека нельзя научить, развить, воспитать; он может только научить себя сам, т. е. научиться, развиться, воспитаться .

Формы учебной работы

« Конструкция отрезка процесса обучения, характеризующаяся особыми способами управления, организации и сотрудничества учащихся в учебной деятельности».

Использование парацентрической технологии предполагает

« признание ученика главной действующей фигурой всего образовательного процесса »

Весь учебный процесс строится на основе этого главного положения.

Основные формы учебной работы.

групповая

фронтальная

индивидуальная

Управление всем составом класса

Самостоятельное выполнение заданий

Парная

Звеньевая

Бригадная др.

Коллективная

(совместные поиски)

Модель адаптивной системы обучения (АСО )

Учитель обучает всех учеников

• Учитель работает индивидуально.
• ( в двух режимах): -обучает новому; индивидуально работает. Эта работа заключается в двух подходах:
• 1. управление с/р учащихся (осуществление включенного контроля);
• 2. индивидуальная работа (осуществление отключенного контроля).

• Ученики работают самостоятельно.
• ( учащиеся в АСО работают в 3 режимах)
• 1. совместно с учителем;
• 2. с учителем индивидуально;
• 3.самостоятельно под руководством учителя.

Карточка для работы в паре « Ученик –учитель» Тема: « Арифметический корень натуральной степени» 10 кл.)

• Вариант №1.
• 1. Вычислите:

• 2. решите уравнение:5х⁵ =-160.

• 3.При каких значениях (х ) имеет смысл выражение:

• 4.Вычислите:

• 5. Упростите выражение:

• Вариант №2.
• 1.Решите уравнение:2х⁶=128.
• 2. Вычислите:

• 3.Упростите выражение:

• 4.При каких значениях х имеет смысл выражение:

• 5. Вычислите:

Карточка для работы в паре « Ученик –учитель» Тема « Свойства степени с рациональным показателем» 10кл.

Упрости выражение. Сформулируйте правило, используемое при упрощении.

Определите, какие преобразования нужно выполнить в каждом из предложенных выражений, чтобы упростить его:

Разложите на множители используя формулы сокращённого умножения:

Карточка для работы в динамической паре( 8кл.,тема: « Определение квадратного уравнения. Неполные квадратные уравнения».)

Карточка №1.

Карточка №1.

• Как называются числа а и в в квадратном уравнении?
• В каком случае квадратное уравнение называется неполным?
• Сколько корней имеет квадратное уравнение:

Ответы.

1.Число а называется первым коэффициентом, число в- вторым коэффициентом квадратного уравнения.

Ответ объясните.

2. Если хотя бы один из коэффициентов в или с квадратного уравнения равен нулю, то квадратное уравнение называется неполным.

3. Это уравнение не имеет корней, т.к. квадрат любого числа неотрицателен.

Обратная сторона карточки

(для опрашивающего)

Лицевая сторона карточки

(для отвечающих)

Карточка для работы в динамической паре (Геометрия -8 кл, тема: « Теорема Пифагора»)

Обратная сторона карточки

(для опрашивающего)

1.Каким отношением можно записать синус угла В? (ответ: SinВ =в/с )

2. Какой компонент полученной формулы неизвестен? ( ответ: Неизвестен катет в, который легко можно найти, пользуясь этой формулой: в =с*SinВ = 15*0,6=9 (м).

3. Как найти а? ( ответ: по теореме Пифагора:

• Лицевая сторона карточки
• (для отвечающих)
• Дано: ∆ АВС (
• С=15 м; Sin В= 0,6.
• Найдите: а,в.

Дифференцированный подход в обучении

А

В

С

Сильные учащиеся , с глубокими, прочными знаниями, умеющие аргументировать, обобщать методы решения задач.

Средние учащиеся , обладающие хорошими знаниями основных фактов, но затрудняющиеся при решении творческих задач.

Слабые учащиеся , обладающие минимум знаний, умений и навыков достаточных для их применения по образцу.

На уроке по изучению нового материала

Те ученики, которые ещё не усвоили новую тему достаточно хорошо.

Учащиеся, которые считают, что уже поняли новый материал и могут работать самостоятельно .

1 группа

2 группа

Самостоятельная и коллективная работа

Урок закрепления изученного материала учащиеся работают по группам

А

В

Получают нестандартные или более сложные и объёмные задания.

С

Задания

необязательного уровня.

Задания обязательного уровня.

4х(х+2). Доказательство: а) 2(а+1)+а 1.Раскроем скобки: б) (х-3)(х-5) 4х 2 +2х+6х+34х 2 +8х; 4х 2 +8х+3 4х 2 +8х . Составить разность левой и правой частей и сравнить её с нулём. Левая часть правая часть в) (у+5) 2 -у(у+10) 0; г) (6х-1)(6х+1) 2. Составим разность левой и правой частей: 4х 2 +2х+6х+3-(4х 2 +8х)0, 4х 2 +8х+3-4х 2 -8х0, Сделать вывод. д) (у-2) (у-з) у(у-5); 30. 3 . Вывод : т.к. разность есть число положительное, то выражение, стоящее в левой части неравенства, больше выражения, стоящего в правой части, ч.т.д. е) (х-1)(х-3) х(х-4); ж) у 2 +1 2(3у-4); З) х 2 +5 10(х-2)." width="640"

правило

образец

При доказательстве числовых неравенств надо:

задания

Доказать неравенство:

Доказать неравенство:

(2х+з)(2х+1)4х(х+2).

Доказательство:

а) 2(а+1)+а

1.Раскроем скобки:

б) (х-3)(х-5)

4х 2 +2х+6х+34х 2 +8х;

4х 2 +8х+3 4х 2 +8х .

• Составить разность левой и правой частей и сравнить её с нулём.

Левая часть правая часть

в) (у+5) 2 -у(у+10) 0;

г) (6х-1)(6х+1)

2. Составим разность левой и правой частей:

4х 2 +2х+6х+3-(4х 2 +8х)0,

4х 2 +8х+3-4х 2 -8х0,

• Сделать вывод.

д) (у-2) (у-з) у(у-5);

30.

3 . Вывод : т.к. разность есть число положительное, то выражение, стоящее в левой части неравенства, больше выражения, стоящего в правой части, ч.т.д.

е) (х-1)(х-3) х(х-4);

ж) у 2 +1 2(3у-4);

З) х 2 +5 10(х-2).

Уравнения, содержащие модуль.

(8класс)

Правило

образец

1. а= { а, если а≥0,

1. Обязательный уровень. lЗ-4х l=3

-а, если а

Если 3-4х≥0, тогда 3-4х=3, если 3-4х

2. При решении уравнений , содержащих неизвестное под знаком абсолютной величины нужно: -разбить всю область допустимых значений на интервалы точками, в которых значение модуля равно нулю;- и на каждом из интервалов свести уравнение к обычному алгебраическому.

-4х=3-3, -4х=-3-3,

-4х=0, -4х=-6,

х=0, х=1,5.

Ответ: х=0, х=1,5.

2. Необязательный уровень. |2х-5|=х-1.

Если 2х-5≥0, х≥5/2, если 2х-5

Х € (-∞ ,5/2)U[5/2 ,+∞ ). 2х-5=х-1, 2х-5=-(х-1).

х=4, х=2.

значения х принадлежат данному промежутку, значит являются решением. Ответ: х=2,х=4.

Уравнения, содержащие модуль . (Продолжение 11-12 класс)

Образец

задания

Пример 1 . |х-з|-|2х-1|=2, |х-3|=0, |2х-1|=0,

а) |х|+|х-2|=2.

х=3, х=-1/2.

Область определения : (-∞; -1/2)U[-1/2;3)U[3 ;+∞) .

а) (-∞ ; -1/2): |х-3|=-х+3, |2х+1|=-2х+1,

б) |х|=х+2,

УР-Е: -х+3-(-2х+1)=2

-х+3+2х-1=2

в) |-х+2|=2х-1,

х=-2, входит в область определения.

г) |х-1|+|х-2|=1,

б)[-1/2;3]: |х-3|=-х+3, |2х+1|=2х+1,

УР-Е: -х+3-2х-1=2,

д) |х-1|+|х+2|-|х-3|=4,

х=0, входит в область определения.

в) [3; +∞ ): |х-3|=х-3, |2х+1|=2х+1,

УР-Е: х-3-2х-1=2,

е) |з-|х||=|2-х|-3.

х=-6, не входит в область определения.

Ответ: х=-2, х=0.