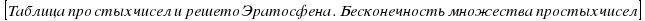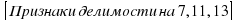РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ ПО ФГОС
5 КЛАСС
(физико-математический профиль)
Автор-составитель
Скорук Марина Васильевна,
учитель математики
МАОУ «Центр образования № 13
имени Героя Советского Союза
Н.А.Кузнецова»,г.Тамбов
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по математике для 5 класса (физико-математический профиль) составлена в соответствии с Федеральным государственным образовательным стандартом основного общего образованиям на основе Фундаментального ядра содержания общего образования, Требований к результатам освоения основной образовательной программы основного общего образования. За основу взята Примерная программа основного общего образования по математике, а также авторская программа по математике Л.Г.Петерсон «Учусь учиться» для 5 – 6 классов средней школы по образовательной системе деятельностного метода обучения «Школа 2000».
В рабочей программе учтены идеи и положения Концепции развития математического образования в Российской Федерации (утв. распоряжением Правительства РФ от 24.12.2013), Программы развития и формирования универсальных учебных действий, которые обеспечивают овладение ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, в том числе коммуникативных качеств личности.
Рабочая программа составлена в соответствии с Основной образовательной программой основного общего образования МАОУ «Центр образования № 13 имени Героя Советского Союза Н.А.Кузнецова».
Рабочая программа по математике для 5 класса представляет собой целостный документ, включающий пояснительную записку, планируемые результаты изучения предмета, содержание учебного предмета, тематическое планирование, учебно-методическое и материально-техническое обеспечение.
Программа соответствует учебнику Г.В.Дорофеева, Л.Г.Петерсон «Математика. 5 класс» (М.: Издательство «Ювента», 2013)
Данная программа конкретизирует содержание предметных тем, дает примерное распределение учебных часов по разделам курса, рекомендуемую последовательность изучения тем и разделов с учетом межпредметных и внутрипредметных связей, логики учебного процесса, возрастных особенностей учащихся.
Предлагаемая программа выполняет две основные функции:
информационно-методическая - позволяет получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся 5 класса средствами математики;
организационно-планирующая – предусматривает выделение этапов обучения, определения качественных и количественных характеристик учебного материала на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Многим людям в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, составлять несложные алгоритмы, читать информацию, представленную в виде графиков, схем, диаграмм и т.п. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация научных знаний, разнообразной социальной, экономической, политической информации. Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: простанственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей.
Без базовой математической подготовки невозможно достичь высокого уровня образования, так как все больше специальностей связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.) Следовательно, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе не менее важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются дедукция и индукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. С помощью объектов математических умозаключений и правил их конструирования вскрывается механизм логических построений, вырабатываются умения формулировать, обосновывать и доказывать суждения, тем самым развивается логическое мышление.
Математике принадлежит ведущая роль в развитии алгоритмического мышления, формировании умения дейстовать по заданным алгоритмам, конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Использование в математике нескольких математических языков дает возможность развивать у учащихся точную, экономную, информативную устную и письменную речь, умения подбирать наиболее подходящие языковые средства (в частности, символьные, графические).
Математическое образование вносит свой вклад в формирование общей культуры человека. Ее необходимым компонентом является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и дествитетльности, представление о предмете и методе математики, его оличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, развитию воображения, пространственных представлений. Изучение истории развития математики дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представление о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Изучение математики в 5 классе направлено на достижение следующих целей:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
развитие умения контролировать процесс учебной математической деятельности;
развитие математических способностей и интереса к математическому творчеству;
развитие способностей к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
развитие познавательных интересов, интеллектуальных и творческих способностей учащихся;
развитие способностей к самостоятельному приобретению новых знаний и практических умений, умения управлять своей познавательной деятельностью.
овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи формулируются в соответствии с ФГОС и с учетом особенностей общеобразовательного учреждения. Задачами изучения курса математики в 5 классе являются:
систематическое развивать понятие числа;
вырабатывать умения выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, применять изученные алгоритмы для решения уравнений, задач арифметическим и алгебраическим способами, рационализации вычислений;
подготовить учащихся к изучению систематических курсов алгебры и геометрии..
ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
Изучение математики в 5 классе призвано способствовать приобретению практических навыков, необходимых для повседневной жизни. Основу курса составляет развитие понятия числа и формирование крепких вычислительных навыков. В 5 классе происходит постепенное расширение множества натуральных чисел путем введения обыкновенных дробей с одинаковыми показателями и десятичных дробей. Курс строится на наглядно-интуитивном уровне с привлечением практического опыта учащихся и примеров из жизни. Происходит постепенное увеличение теоретического материала, требующего элементы дедуктивных рассуждений для обоснования математических утверждений. Это готовит учащихся к широкому использованию дедуктивных методов на следующих этапах изучения математики.
В ходе освоения содержания курса учащиеся получают возможность развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру.
Изучение ведется по учебнику «Математика. 5 класс» Г.В. Дорофеева и Л. Г. Петерсон, который в достаточной степени изменен в плане содержания образования по сравнению с традиционными учебниками и продолжает линию учебников по математике начальной школы по программе «2000» и программе «2100» тех же авторов, что учитывает преемственность с начальным периодом обучения, индивидуальные потребности школьников и обеспечение возможностей развития математических способностей обучающихся.
В основе обучения лежит системно-деятельностный подход, организация разнообразной учебной деятельности. Предложенное в учебнике интенсивное изучение материала позволяет широко использовать приёмы активизации учебной деятельности школьников, связанные с игровыми и занимательными моментами, принцип опережающего обучения. Например, тема «Проценты» вводиться в 3 классе, но она отрабатывается в 5 и 6 классах, постоянно усложняясь и расширяясь.
Программа изучения материала представлена так, что действия с десятичными и обыкновенными дробями изучаются в 5 классе. Существенное место в изучении курса занимают текстовые задачи, основными функциями которых являются развитие логического мышления, иллюстрация практического применения математических знаний. Во время решения задач учащиеся учатся строить и использовать математические модели. Последовательно изучаются все типы задач на дроби, проценты, движение; идёт сравнительная характеристика. Одной из главных целей обучения остается организация математической деятельности учащихся, их знакомство с математическим методом исследования реальной действительности. Систематически рассматривается решение нестандартных задач, которых много в учебнике.
Учебный материал, касающийся выражений, величин, уравнений и неравенств, геометрических фигур, носит пропедевтический характер. Ознакомление с ним готовит учащихся к осознанному изучению алгебры и геометрии. Учащиеся должны получить представления об использовании букв для записи законов арифметических действий, формул, научиться находить значения простых буквенных выражений, составлять по условию задачи несложные уравнения и решать их на основе зависимостей между компонентами арифметических действий.
В курсе математики изучается наглядно-деятельностная геометрия, направленная на расширение геометрического кругозора учащихся. Геометрический материал, вплетаясь в мир чисел, гармонично влияет на изучение материала.
В курсе математики 5 класса происходит развитие умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Раздел «Элементы логики, комбинаторики и теории вероятностей» — компонент содержания образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности – умения воспринимать и критически анализировать информацию, представленную в различных формах, принимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
Особенности образовательного процесса
Законом «Об образовании в РФ» учителю предоставляется право самостоятельного выбора методических путей и приемов решения образовательных и воспитательных задач. Рациональная система методов и приемов обучения, ее оптимизация с учетом возрастных особенностей учащихся, уровня их математической подготовки является важным условием правильной организации учебно-воспитательного процесса. В зависимости от указанных факторов учителю необходимо сбалансировать сочетание традиционных и инновационных методов обучения, оптимизировать применение объяснительно-иллюстративных и эвристических методов, рационально использовать современные технические средства. Учебный процесс необходимо ориентировать на оптимальное сочетание устных и письменных видов работы как при изучении теории, так и при решении задач. Внимание учителя должно быть направлено на развитие у учащихся навыков умственного труда (планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов), культуры устной и письменной математической речи.
В ходе изучения курса математики 5 класса обучающиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач: формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопостовлять его с собственными математическими знаниями. Обучающиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, рецензии.
Принципиальным положением организации математического образования становится дифференциация и индивидуализация обучения. Это означает, что осваивая курс математики, одни школьники в своих результатах ограничиваются уровнем базовой обязательной подготовки, зафиксированным в образовательном стандарте, другие, в соответствии со своими склонностями и способностями достигают более высоких результатов. при этом каждый имеет право самостоятельно решить ограничиться базовым уровнем или двигаться дальше. Развитие интереса к математике является важнейшей задачей учителя. Школьники, проявляющие склонности к математике, должны получать индивидуальные задания (в первую очередь нестандартные математические задачи), их следует привлекать к оказанию помощи одноклассникам, к участию в математических кружках, конкурсах, олимпиадах; желательно рекомендовать им дополнительную литературу по предмету.
Особое место в овладении курсом отводится работе по формированию навыков саморегуляции: самоконтроля и самопроверки.
Текущий контроль осуществляется после изучения каждого основного раздела, форма проведения – самостоятельная работа, математический диктант, тест и т.п. В конце года оценка результатов обучения проводится в виде переводного экзамена, который включает задания по основным вопросам курса математики 5 класса.
Формы работы – фронтальная, индивидуальная, групповая, парная.
Педагогическим инструментом реализации поставленных целей в курсе математики 5 класса являются следующие технологии - технология деятельностного метода, технология проблемного диалога, технология продуктивного чтения, технология развития критического мышления, технологии оценивания.
МЕСТО УЧЕБНОГО ПРЕДМЕТА В УЧЕБНОМ ПЛАНЕ
Базисный учебный (образовательный) план на изучение математики в основной школе отводит 5 учебных часов в неделю в течение учебного года, всего 175 уроков.
Данная программа предназначена для классов физико-математического профиля, где на изучение предмета отводится на 1 час больше за счет компонента образовательного учреждения: в 5 классе – до 6 часов в неделю, 210 часов в год.
Методической особенностью курса «Математика» для классов физико-математического профиля является расширение традиционных учебных тем за счёт теоретико-множественной, вероятностно-статистической и историко-культурной линий. Содержание материала, вынесенного на изучение за счет вариативной части базисного учебного плана не дублирует, а дополняет материал основного курса. За счёт дополнительных часов углубляется практическая направленность изучения тем «Задачи с практическим содержанием», «Вопросы теории делимости», «Комбинаторика» и некоторые другие.
В программе предусмотрен резерв свободного учебного времени для реализации авторских подходов, использования разнообразных форм организации учебного процесса, внедрения современных методов обучения и педагогических технологий.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ ПРЕДМЕТА
В результате освоения предметного содержания по математике у учащихся, оканчивающих 5 класс, формируются:
личностные результаты:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
формирование целостного мировоззрения, представление о математической науке как сфере человеческой деятельности, об этапах развития, о её значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
ответственное отношение к учению, заинтересованность в приобретении и расширении математических знаний и способов;
воля и настойчивость в достижении цели;
формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению, мировоззрению, готовности и способности вести диалог с другими людьми и достигать в нём взаимопонимания;
освоение социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах в пределах возрастных компетенций;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, взрослыми в процессе образовательной, общественно полезной, учебно-исследовательской, творческой и других видов деятельности.
метапредметные результаты:
регулятивные универсальные учебные действия
умение самостоятельно обнаруживать и формулировать учебную проблему, определять цель учебной деятельности, выбирать тему проекта;
выдвигать версии решения проблемы, осознавать (и интерпретировать в случае необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);
работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план);
умение оценивать правильность выполнения учебной задачи, ее объективную трудность и собственные возможности её решения;
в диалоге с учителем совершенствовать самостоятельно выработанные критерии оценки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности;
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.
познавательные универсальные учебные действия:
умение видеть математическую задачу в контексте проблемной ситуации, в других дисциплинах, в окружающей жизни;
формирование первоначальных представлений об идеях и методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов;
умение понимать и использовать математические средства наглядности (диаграммы, таблицы, схемы и т.п.) для иллюстрации, интерпретации, аргументации;
умения устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения (индуктивные, дедуктивные, по аналогии), делать выводы;
умения создавать, применять и преобразовывать знакосимволические средства, математические модели и схемы для решения учебных и познавательных задач;
составлять тезисы, различные виды планов (простых, сложных и т.п.); преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);
вычитывать все уровни текстовой информации;
умение использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей, выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.
коммуникативные универсальные учебные действия:
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы;
работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов;
отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;
в дискуссии уметь выдвинуть контраргументы;
учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;
уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.
Предметные результаты обучения:
В результате изучения курса математики 5 класса:
ученик научится:
записывать и читать математические выражения;
обосновывать суждения, математические утверждения;
составлять выражения по тексту задачи, переводить условия задач на математический язык и работать с математическими моделями пяти типов,
решать уравнения методом проб и ошибок, методом перебора, на основе зависимостей между компонентами;
точно и грамотно выражать свои мысли в устной и письменной речи, применять математическую терминологию и символику, использовать различные языки математики (словесный, символьный, графический, табличный);
работать с математическим текстом (анализировать, извлекать необходимую информацию);
находить НОК и НОД , степень числа;
применять признаки делимости на 10, на 2 и на 5, на 3 и на 9, на 4 и на 25;
разкладывать числа на простые множители;
сокращать дроби, приводить к новому знаменателю, к общему знаменателю;
записывать частное в виде дроби, выделять целую часть из неправильной дроби, переводить смешанные числа в неправильную дробь, сравнивать дроби;
выполнять сложение и вычитание дробей, смешанных чисел;
выполнять умножение и деление обыкновенных дробей;
находить дробь от числа и число по его дроби в простейших случаях;
читать и записывать десятичные дроби;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, находить в несложных случаях значения степеней с целыми показателями; находить значения числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и дробями; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера; устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
сравнивать, складывать и вычитать десятичные дроби;
умножать и делить десятичные дроби на 10, 100, 1000
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
проводить несложные практические расчеты с использованием при необходимости калькулятора, компьютера;
решать текстовые задачи;
работать с информацией, представленной в виде несложных таблиц и диаграмм;
представлять собранные данные в табличной форме, извлекать информацию из таблиц и диаграмм.
ученик получит возможность научиться:
применять аппарат уравнений для решения задач из различных разделов курса;
овладеть основными способами представленяи и анализа статистических данных;
решать комбинированные задачи на нахождение дроби от числа и числа по значению дроби;
строить и читать таблицы и круговые диаграммы, анализируя условие задачи математического и прикладного характера;
математически моделировать практические ситуации в простейших случаях.
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА
Данная программа нацелена на повышенный уровень математической подготовки учащихся. Расширение содержания математического образования дает возможность существенно обогатить круг решаемых математических задач. Курсивом в тексте выделен материал, который подлежит изучению в классах физико-математического профиля, но не включается в Требования к уровню подготовки выпускников.
Обобщение и систематизация материала, изученного в начальной школе ( 8 часов)
Глава 1. Математический язык ( 36 часов)
Математические выражения. Запись. Чтение и составление выражений. Значение выражений. [Факториал].
Математические модели. Перевод условий задачи на математический язык. Работа с математическими моделями. Метод проб ошибок. Метод перебора.
Язык и логика. Высказывания. Общие утверждения. Утверждения о существовании – «хотя бы один». Способы доказательства общих утверждений. Введение обозначений.
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – сформировать представление о математическом методе исследования реального мира; повторить известные из начальной школы методы работы с математическими моделями; познакомить с методом проб и ошибок и методом перебора.
Глава 2. Делимость натуральных чисел ( 45 часов)
Делители и кратные. Простые и составные числа. Особый статус единицы. 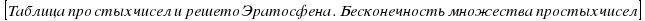
Основные свойства делимости натуральных чисел: свойства делимости как отношения, свойства делимости, связанные с арифметическими действиями. Делимость произведения. Делимость суммы и разности.
Признаки делимости на 10, 100, 1000 и т.д., на 2 и на 5, на 3 и на 9, на 4 и на 25. 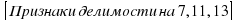
Разложение на простые множители. Наибольший общий делитель и наименьшее общее кратное. Различные способы нахождения наибольшего общего делителя и наименьшего общего кратного. [Связь между наибольшим общим делителем, наименьшим общим кратным и произведением двух чисел].
Степень числа. Простейшие свойства степеней. Дополнительные свойства умножения и деления. Взаимно простые числа. Деление с остатком.
Равносильность предложений. Определения.
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – повторить знания о натуральных числах и их свойствах; познакомить с понятиями, связанными с делимостью чисел; подготовить теортическую основу для изучения обыкновенных дробей.
Глава 3. Дроби ( 54 часов)
Натуральные числа и дроби. Обыкновенная дробь. Числитель и знаменатель дроби. Правильные и неправильные дроби. Смешанные числа. Целая и дробная части смешанного числа. Алгоритмы перевода неправильной дроби в смешанное число и смешанного числа в неправильную дробь.
Основное свойство дроби. Приведение дробей к общему знаменателю. Условие равенства дробей. Сравнение дробей.
Арифметика дробей и смешанных чисел: сложение, вычитание, умножение и деление. Примеры вычислений с дробями. Задачи на дроби (нахождение части от целого и целого по его части). Задачи на совместную работу.
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – сформировать понятия дроби, правильной и неправильной дроби, смешанного числа; выработать прочные навыки чтения, записи, сравнения и вычислений с обыкновенными дробями и смешанными числами; познакомить с новыми приемами решения задач на дроби;повторить задачи на совместную работу.
Глава 4. Десятичные дроби ( 45 часов)
Новая запись чисел. Десятичные и обыкновенные дроби. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде конечной или бесконечной десятичной. [Критерий возможности перевода обыкновенной дроби в десятичную]. Приближенные равенства. Округление чисел. Сравнение десятичных дробей. [Мотивы изобретения десятичных дробей: стандартизация системы измерения величин, аналогия с десятичной системой счисления натуральных чисел]. Сложение и вычитание десятичных дробей. Умножение и деление десятичных дробей на 10, 100, 1000 и т.д. Умножение десятичных дробей. Деление десятичных дробей.
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – сформировать понятие десятичной дроби, выработать прочные навыки чтения, записи, сравнения и вычислений с десятичными дробями, навыки преобразования и действий с именованными числами; вывести правила округления чисел, условия преобразования дробей из десятичной в обыкновенную и обратно, сформировать умение применять эти правила в процессе преобразования дробей.
Глава 5. Элементы логики, статистики, комбинаторики, теории вероятностей ( 9 часов)
Сбор и обработка статистической информации о явлениях окружающей действительности. Опросы общественного мнения как сбор и обработка статистической информации.
Решение простейших логических задач.
Круговые диаграммы. Чтение информации, содержащейся в круговой диаграмме. Построение круговых диаграмм.
Решение простейших комбинаторных задач.
Понятие о вероятности случайного события.
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – получить представление об основных способах получения, представления и анализа статистиченских данных; о статистических закономерностях в реальном мире мире и о различных способах их изучения, о вероятностных моделях.
Итоговое повторение ( 13 часов)
Решение задач
О с н о в н а я с о д е р ж а т е л ь н а я ц е л ь – повторить и систематизировать материал курса математики 5 класса
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
С ОПРЕДЕЛЕНИЕМ ОСНОВНХ ВИДОВ ДЕЯТЕЛЬНОСТИ
| № п/п | Название темы, раздела | Кол-во часов | Кол-во к/р | Характеристика основных видов деятельности обучающихся(на основе учебных действий) |
|
| Обобщение и систематизация материала, изученного в начальной школе | 8 | 1 | Находить значения натуральных выражений, используя изученные алгоритмы. Решать текстовые задачи. Решать уравнения на нахождение компонентов. |
| 1 | Математический язык | 36 | 2 | Записывать, читать и составлять математические выражения. Находить значения числових и буквенных выражений. Объяснять, что такое и Вычислять значение факториала. Переводить условие задачи на математический язык. Составлять по условию задачи математическую модель и работать с ней; интерпретировать полученный результат. Составлять выражения по тексту задачи, переводить условия задач на математический язык и работать с математическими моделями пяти типов. Решать уравнения методом проб и ошибок, методом перебора, на основе зависимостей между компонентами. Использовать в работе метод проб и ошибок, метод перебора. Распознавать высказывания и общие утверждения, выражать их в речи разными способами. Распознавать высказывания о существовании, выражать их в речи разными способами, доказывать с помощью соответствующего примера и доступным способом опровергать. Доказывать общие утверждения способом перебора и введением обозначений. |
| 2 | Делимость натуральных чисел | 45 | 2 | Объяснять, что такое наибольший общий делитель, наименьшее общее кратное. Знать алгоритм нахождения НОД, НОК. Находить НОД, НОК по алгоритму. Сокращать дробь, находя наибольший общий делитель. Иметь представление о о признаках делимости, о признаках делимости произведения, о признаках делимости суммы и разности чисел, о свойствах делимости чисел. Выполнять действия, применяя признаки делимости суммы и разности. Доказывать признаки делимости суммы и разности чисел на число. Понимать и формулировать свойства делимости суммы и разности чисел на число, иллюстрировать примерами, доказывать утверждения, обращаясь к соответствующим свойствам. Оперировать символикой деления числа нацело, без остатка. Иметь представление о признаках делимости на 2, 3, 4, 5, 9, 10 и 25. Проверять делимость числа на числа 2, 5, 10, 4, 25, 3, 9, а так же сокращать большие дроби, используя признаки делимости. Объяснять, какие числа называются простыми, составными, взаимно простыми числами, числами-близнецами, что такое каноническое разложение. Подбирать пары взаимно простых чисел. Формулировать алгоритм разложения на простые множители, основную теорему арифметики. Различать простые и составные числа, раскладывать составные сила на простые множители. Записывать разложение числа на простые множители в канонической форме. Находить общие делители и общие кратные с помощью разложения чисел на простые множители. Приводить дроби к общему знаменателю, решая примеры на вычисления и уравнения. |
| 3 | Дроби | 54 | 3 | Читать и записывать обыкновенные дроби. Называть числитель и знаменатель дроби и объяснять, что они показывают. Записывать частное в виде дроби, выделять целую часть из неправильной дроби, переводить смешанные числа в неправильную дробь, сравнивать дроби. Сокращать дроби, приводить к новому знаменателю, к общему знаменателю. Выполнять сложение и вычитание дробей, смешанных чисел. Выполнять умножение и деление обыкновенных дробей. Находить дробь от числа и число по его дроби. Решать простейшие задачи на нахождение дроби от числа и числа по значению дроби. |
| 4 | Десятичные дроби | 45 | 2 | Читать и записывать десятичные дроби. Иметь представление о десятичных разрядах. Переводить десятичные дроби в обыкновенные и наоборот. Округлять десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений. Выражать данные значения длины, массы, площади, объема в виде десятичных дробей. Сравнивать, складывать и вычитать десятичные дроби. Умножать и делить десятичные дроби на 10, 100, 1000. Выполнять арифметические действия с десятичными дробями. Решать текстовые задачи на сложение и вычитание, данные в которых выражены десятичными дробями. Выполнять задания на все действия с натуральными числами, обыкновенными и десятичными дробями. Применять свойства умножения и деления десятичных дробей при упрощении числовых и буквенных выражений и нахождении их значений. |
| 5 | Элементы логики, статистики, комбинаторики, теории вероятностей | 9 | 1 | Строить круговые диаграммы. Читать информацию, записанную с помощью линейных, круговых диаграмм. Использовать простейшие способы представления и анализа статистических данных.Приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы. |
|
| Итоговое повторение | 13 | 1 | Выполнять вычисления значений натуральных и дробных выражений, используя изученные алгоритмы. Выводить признаки делимости, применить признаки делимости при сокращении дробей. Решать задачи на нахождение дроби от числа и числа по его дроби, на движение и т.д. Составлять математическую модель реальной ситуации. |
|
| Всего | 210 | 12 |
|
УЧЕБНО-МЕТОДИЧЕСКОЕ И МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА
Для учителя
Федеральный государственный образовательный стандарт основного общего образования/Минобрнауки РФ. – М.: Просвещение, 2011. – 48 с. – (Стандарты второго поколения).
Фундаментальное ядро содержания общего образования / Под. Ред. В. В. Козлова, А. М. Кондакова. – М.: Просвещение, 2009. – 48 с. (Стандарты второго поколения).
Примерные программы по учебным предметам. Математика 5-9 классы: проект. – 3-е изд. Перераб. – М.: Просвещение, 2011. – 64 с. – (Стандарты второго поколения).
«Математика: учебник для 5 класса Г.В.Дорофеев, Л.Г. Петерсон - М.: Издательство «Ювента», Москва 2013 г.
Кубышева М.А. Самостоятельные и контрольные работы по курсу математики для 5–6 классов. – М.: УМЦ «Школа 2000...», 2011г.
Математика. Методические рекомендации к учебнику. 5 класс. (ФГОС)
Петерсон Л.Г., Грушевская Л.А., Кубышева М.А., Рогатова М.В. - М.: Издательство «Ювента», Москва 2013 г.
Устные упражнения на уроках математики. 5 класс. Петерсон Л.Г., Липатникова И.Г. (2008)
Петерсон Л.Г., Грушевская Л.А. Построй свою математику. Блок-тетрадь эталонов для 5 класса. 5 класс. (2007 г)
Петерсон Л.Г., Грушевская Л.А., Мазуркина С.Е. Эталоны-помощники учителей и учеников. 1-6 классы. Методические рекомендации к учебному пособию «Построй свою математику» (2007 г)
Контрольно-измерительные материалы Математика 5 класс / Сост.Л.П.Попова. – М.: Вако,2012 г.
Анфимова Т.Б. Математика Внеурочные занятия 5-6 классы. – М.: ИЛЕКСА,2011 г.
История математики в школе: IV-VI кл. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
Для учащихся
«Математика: учебник для 5 класса Г.В.Дорофеев, Л.Г. Петерсон - М.: Издательство «Ювента», Москва 2013 г.
Кубышева М.А. Самостоятельные и контрольные работы по курсу математики для 5–6 классов. – М.: УМЦ «Школа 2000...», 2011г.
Петерсон Л.Г., Грушевская Л.А. Построй свою математику. Блок-тетрадь эталонов для 5 класса. 5 класс. (2007 г)
Петерсон Л.Г., Грушевская Л.А., Мазуркина С.Е. Эталоны-помощники учителей и учеников. 1-6 классы. Методические рекомендации к учебному пособию «Построй свою математику» (2007 г)
Контрольно-измерительные материалы Математика 5 класс / Сост.Л.П.Попова. – М.: Вако,2012 г.
За страницами учебника математики: Пособие для учащихся 5-6 классов средней школы. – М.: Просвещение, 1989 – 287 с.
Задачи для внеклассной работы по математике (5-11 классы) / А.В. Мерлин, Н.И. Мерлина/ Учебное пособие, 2-е изд., испр. и доп. Чебоксары: Изд-во Чувашского университета, 2002.
Кривоногов В. В. Нестандартные задания по математике: 5-11 классы. М. Издательство «Первое сентября», 2003.
Шарыгин И.Ф., А.В. Шевкин. Задачи на смекалку: Учебное пособие для 5-6 кл. общеобразовательных учреждений. М.: Просвещение, 2003. – 95 с.
Интернет-ресурсы:
Министерство образования и науки РФ. http://www.mon.gov.ru/
Федеральное государственное учреждение «Государственный научно-исследовательский институт информационных технологий и телекоммуникаций». http://www.informika.ru/
Тестирование on-line: 5–11 классы. http://www.kokch.kts.ru/cdo/
Путеводитель «В мире науки» для школьников. http://www.uic.ssu.samara.ru/~nauka/
Мегаэнциклопедия Кирилла и Мефодия. http://mega.km.ru/
Сайт энциклопедий. http://www.encyclopedia.ru/
Практика развивающего обучения. Сайт методической поддержки УМК «ПРО», www.ziimag.narod.ru
Технические средства обучения:
ПК учителя
Интерактивная доска
Мультимедийный проектор, колонки акустические, экран
Интерактивный диск «Математика 5 класс»
Калькулятор
Учебно-практическое оборудование:
Таблицы по математике для 5 класса
Дидактический раздаточный материал
Набор «Доли и дроби»
12